DFS와 BFS

그래프 순회

그래프 순회는 이름 그대로 그래프상에서 돌아다니는 것으로, 그래프의 모든 정점을 특정 규칙에 따라 방문함으로써 탐색이 가능하다. 대표적인 순회 방법으로는 깊이 우선 탐색(DFS, Depth First Search)과 너비 우선 탐색(BFS, Breadth First Search)가 있다.

깊이 우선 탐색 (DFS)

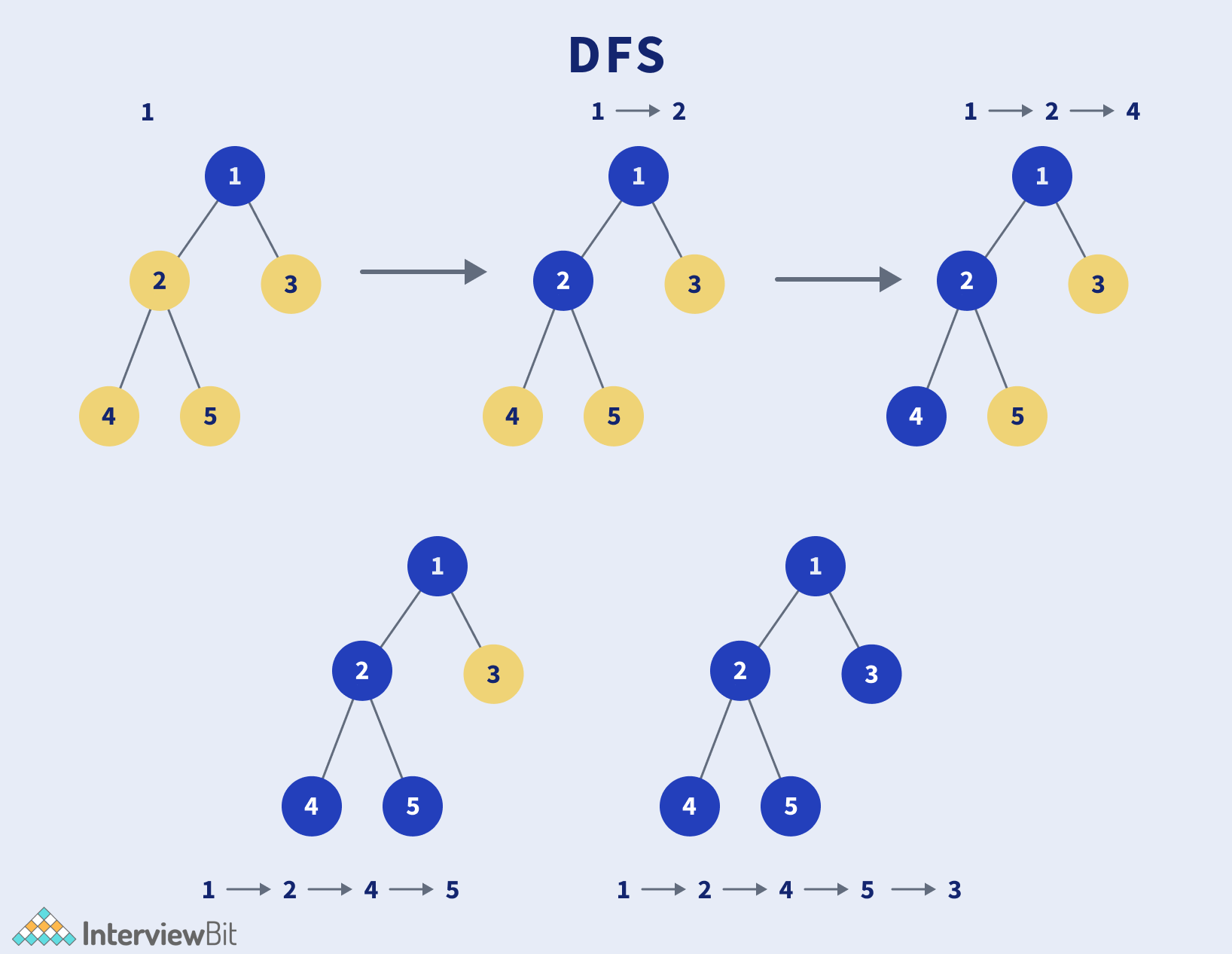
깊이 우선 탐색은 한 정점을 시작으로, 매번 인접한 정점 중 한 곳으로 이동하며 탐색한다. 그래프를 순회하며 정점을 방문할 때마다 인접한 정점 중 한 곳을 따라 우선 탐색을 진행하다가 더이상 방문하지 않은 인접한 정점이 없는 시점에 거꾸로 되돌아가서 다른 경로의 아직 탐색하지 않은 인접 정점을 방문하는 방법이다.

미로 탐색과 유사

깊이 우선 탐색은 스택 자료 구조를 사용하며, 재귀적으로도 구현 가능하다.

스택을 사용했을 때의 처리 방법은 다음과 같다:

1. 시작 정점을 스택에 삽입
2. 스택의 Top에 있는 정점을 pop하여 이에 대한 주변 정점들을 스택에 삽입
3. 스택에 더 이상의 정점이 없을 떄까지 과정 반복

출처: InterviewBit

특징

• 경로의 끝까지 탐색하여 백트래킹을 수행
• 스택을 사용하여 구현 (명시적 스택 or 재귀적 호출)
• 공간 복잡도: O(V)
• 미로 탐색 등에서 보다 효율적

수도코드

스택

def dfs(graph, start):
    visited = set()
    stack = [start]
    while stack:
        node = stack.pop()
        if node not in visited:
            print(node, end=" ")
            visited.add(node)
            stack.extend(graph[node] - visited)

재귀함수

def dfs(graph:Dict, start:int): 
    visited = {i:False for i in graph.keys()} 
    def search(now:int): 
        visited[now] = True 
        for nxt in graph[now]: 
            if not visited[nxt]: 
                search(nxt) 
    search(start)

너비 우선 탐색 (BFS)

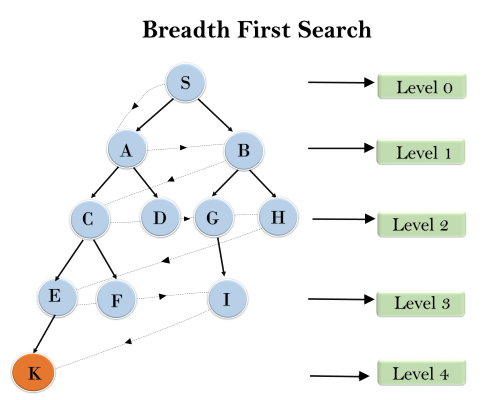
너비 우선 탐색은 시작 정점을 기준으로 거리가 가장 가깝게 인접한 모든 정점을 우선으로 방문한 후, 시작 정점과의 거리가 점점 멀어지는 순서로 인점 정점들을 탐색하는 방법이다. 이 ‘거리’는 시작 정점으로부터 경로의 길이이다.

너비 우선 탐색은 큐 자료구조를 사용하여 인접한 정점들의 리스트를 관리하며, 수행 방법은 다음과 같다:

1. 시작 정점을 큐에 삽입
2. 큐의 앞에서 정점을 pop하여 방문하고, 해당 정점에 인접한 모든 노드를 큐에 추가
3. 큐가 빌 때까지 반복

출처: Javatpoint

특징

• 큐를 사용하여 구현
• 공간 복잡도: O(V)
• 최단 경로 탐색에 적합

수도코드

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        node = queue.popleft()
        if node not in visited:
            print(node, end=" ")
            visited.add(node)
            queue.extend(graph[node] - visited)