분할정복

분할 정복

분할 정복 방법은 하나의 크고 어려운 문제를 두 개 이상의 작고 간단한 하위 문제들로 재귀적으로 분할하고,
이렇게 분할된 문제들을 각각 해결한 후에 해를 결합하여 원래 문제의 해를 구하는 하향식 접근 알고리즘 패러다임이다.

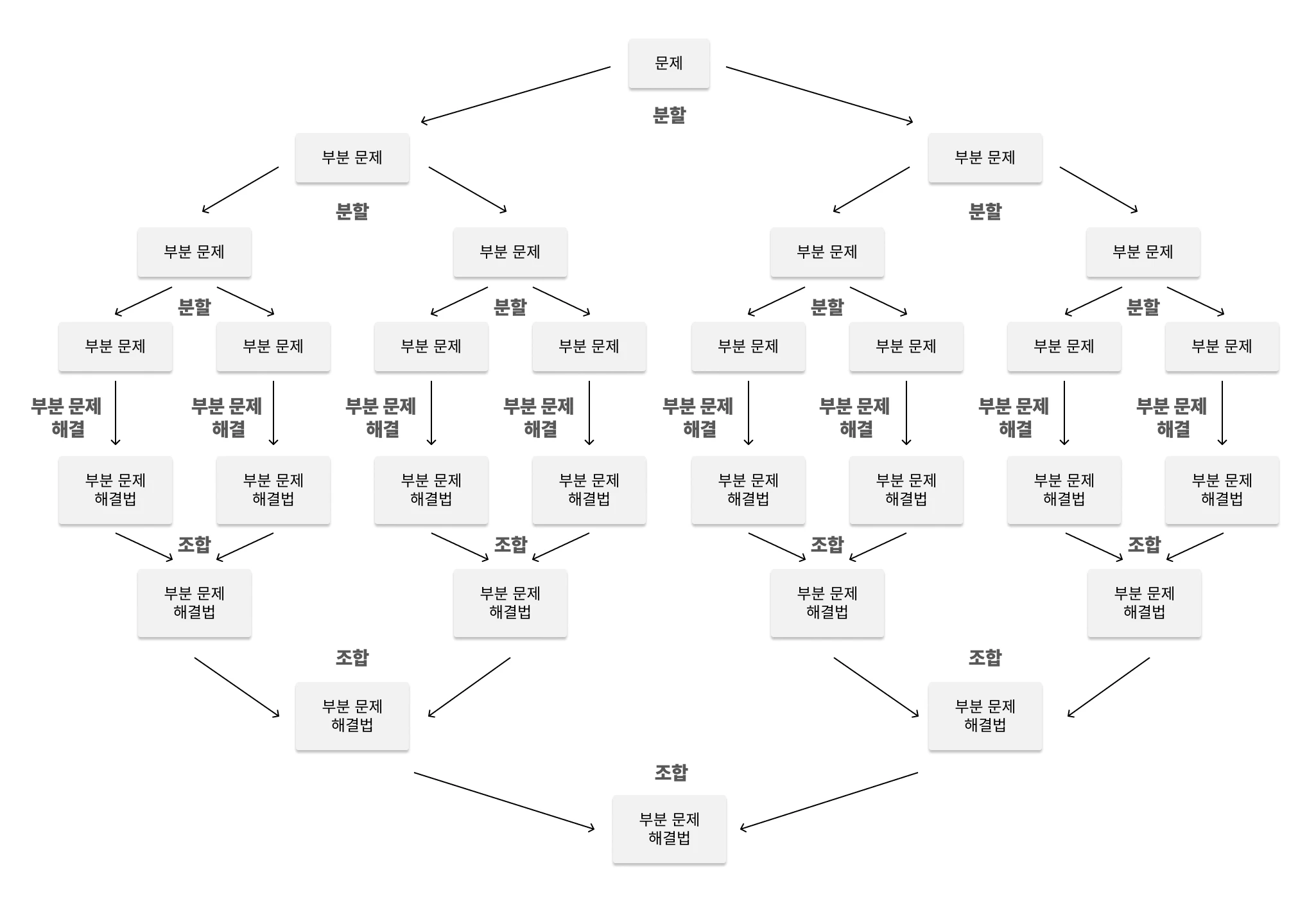
각 호출 시마다 다음과 같은 세 단계의 작업이 이루어진다:

• 분할(divide) : 주어진 문제를 여러 개의 작은 문제로 분할한다.
• 정복(conquer) : 더 이상 분할할 수 없을 때까지 재귀적으로 분할한 후 문제의 해를 구한다.
• 결합(combine) : 작은 문제에 대해 ‘정복’된 해를 결합하여 원래 문제의 해를 구한다.

작게 분할된 문제들은 처리 대상이 되는 입력의 크기가 작아졌을 뿐이며,
이 작아진 문제들은 원래 문제의 성격과 특징을 공유한다.

출처: DISQUIET

장점

분할 정복의 장점으로는 대표적으로 세 가지를 꼽을 수 있다:

1. 효율성

분할 정복 방법을 적용하면 대규모 세트의 알고리즘 시간 복잡성을 크게 줄일 수 있다.
예시로, 이전에 살펴보았던 이진 탐색은 탐색 범위를 반으로 분할하여 해를 찾기 때문에 분할 정복 패러다임을 적용한 알고리즘이다.

이진 탐색

1. 병렬성

하위 문제를 병렬로 처리할 수 있어 다중 코어 프로세서를 활용하게 된다면 계산 속도를 크게 향상시킬 수 있다.

1. 단순성

복잡한 문제를 보다 관리하기 쉬운 작은 문제들로 나누어 알고리즘의 설계와 이해를 단순화시킨다.

응용

분할 정복은 알고리즘 그 자체라기 보다는 알고리즘 설계 패러다임이다.
이게 무슨 말이냐면, 특정 문제를 해결하기 위한 일반적인 방법론이라는 말이며
분할 정복을 기반으로 하여 알고리즘들이 설계된다는 뜻이다.

대표적인 분할 정복 알고리즘으로는 다음이 있다:

• 병합 정렬
• 퀵 정렬
• 이진 탐색

병합 정렬

앞서 언급하였듯이 예시로 병합 정렬을 들 수 있다.

병합 정렬의 시간 복잡도는 O(n log n)으로, 단순 정렬 알고리즘인 버블 정렬의 O(n²) 보다 훨씬 효율적이다.

def merge_sort(arr):
    if len(arr) <= 1:               #더 이 상 분할할 수 없으면 값 반환 
        return arr
    
    mid = len(arr) // 2             #중간을 기준으로 두 개의 부분배열로 나눔
    left = merge_sort(arr[:mid]) 
    right = merge_sort(arr[mid:])

    return merge(left, right)       #나누어진 배열들을 결합하여 반환

def merge(left, right):
    sorted_array = []
    i = j = 0

    while i < len(left) and j < len(right): #두 개의 부분 배열에서 더 작은 값을 새 배열에 삽입
        if left[i] < right[j]:
            sorted_array.append(left[i])
            i += 1
        else:
            sorted_array.append(right[j])
            j += 1

    sorted_array.extend(left[i:])
    sorted_array.extend(right[j:])

    return sorted_array