해시 테이블
해시 테이블
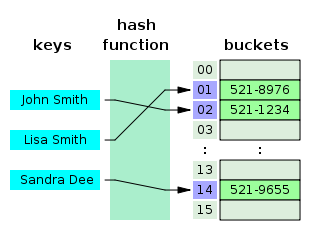
해시 테이블은 각 위치(슬롯)마다 주소가 부여되어 있는 저장공간으로 기본적으로는 배열의 형태로 볼 수 있다.
탐색 키값을 활요하여 해시 테이블의 주소를 계산하면, 이 주소를 통해 원하는 데이터를 해시 테이블에서 직접적이고 빠르게 탐색할 수 있다.
해시 테이블은 평균적으로 O(1)의 시간 복잡도로 데이터를 검색, 삽입, 삭제할 수 있기 때문에 매우 효율적이다.
해시 테이블을 이용하는 방법은 해싱이라 부른다.
“키값 K를 갖는 데이터는 무엇인가?” 라는 질문에 대한 가장 적절한 형태의 탐색 방법이 해시 테이블을 사용하는 것이다.
개념
해시 함수: 데이터를 입력으로 받아 고정된 크기의 해시 값을 반환하는 함수이다.
해시 값: 해시 함수로부터 반환받는 값이다. 버킷: 해시 테이블의 각 슬롯을 버킷이라고 한다.
충돌
서로 다른 두 개의 데이터가 같은 해시 값을 가질 때 충돌이 발생한다.
예를 들어, 데이터를 특정 수 N으로 나눴을 때의 나머지를 해시 값으로 한다면, 여러 데이터는 같은 해시 값을 가질 것이며 충돌이 빈번하게 일어날 것이다.
충돌이 일어나면 여러 가지 이유로 해시 테이블의 성능이 저하되는데, 우선 대표적으로 검색 속도의 저하이다.
앞서 언급했듯이, 해시 테이블의 가장 큰 장점은 평균적으로 O(1)의 시간 복잡도를 갖는다는 점이다.
충돌이 발생하면 충돌 해결 방법에 따라 추가적인 비교 작업이 필요하며, 이는 검색 속도의 저하를 불러온다.
충돌이 일어나면 메모리면에서의 성능 저하 역시 발생한다.
충돌 해결 방법에 따라서 각 버킷에 별도의 자료 구조를 포함시키거나, 테이블 자체의 크기를 증가시켜야 하기 떄문에 메모리 사용이 비효율적이게 된다.
이렇게 띠문에 해시 함수를 잘 짜는 것이 핵심이며, 해시 함수의 형태에 따라 적합한 충돌 해결 방법을 찾는 것 또한 중요하다.
충돌을 해결하기 위해서는 여러 가지가 있는데, 대표적으로 체이닝과 개방주소법이다.
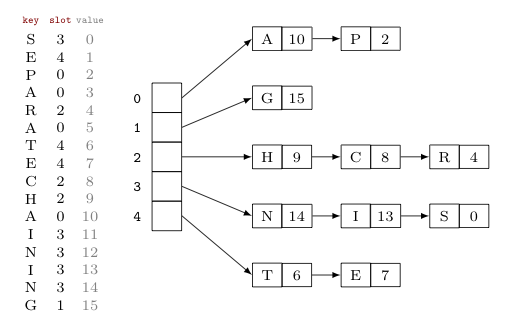
체이닝
체이닝 방법에서는 각 버킷이 연결 리스트를 포함하며, 충돌이 발생하는 경우에 아래와 같이 리스트에 키-값 쌍을 추가한다.
장점으로는 간단한 구현과 동적으로 크기를 조정할 수 있다는 점이다. 여기에 더해, 연결 리스트를 사용하기 때문에 삽입 삭제의 유연성 또한 장점이 된다.
단점으로는, 많은 충돌이 발생하면 리스트가 길어지기 때문에 검색 시간이 증가할 수 있다는 점이다.
개방주소법
충돌이 발생하면 다른 빈 버킷을 찾아 키-값 쌍을 추가한다.
대표적인 개방주소법 활용 방법은 선형 탐사, 이차 탐사, 이중 해싱 등이 있다.
- 선형 탐사: 충돌 발생 시 차례로 검색하여 다음 빈 버킷을 찾는다.
- 이차 탐사: 충돌 발생 시 일정한 규칙에 따라 더 멀리 떨어진 버킷을 찾는다.
- 이중 해싱: 두 번째 해시 함수를 만들어 이를 사용해 새로운 버킷 위치를 계산한다.
특징
해시 테이블은 평균적으로 O(1)의 시간 복잡도로 데이터 검색이 가능하다.
문자열, 숫자 등 다양한 타입의 키를 사용할 수 있다.
일반적으로 배열 크기와 상관없이 많은 메모리를 사용한다.
해시 함수의 품질에 따라 충돌이 빈번하게 일어날 수 있으며, 이는 곧 성능 저하로 이어진다.