크루스칼

크루스칼 알고리즘

최소 비용 신장 트리 (Minimum Spanning Tree, MST)를 구하는 알고리즘으로, 시간 복잡도는 O(E log V)이며, E는 간선(Edge)의 개수, V는 정점(Vertex)의 개수이다.

최소 비용 신장 트리란?

최소 비용 신장 트리, 또는 최소 신장 트리란 주어진 그래프의 모든 정점들이 연결되어 있으면서 사이클이 존재하지 않고, 간선의 가중치 합이 최소로 되는 트리이다.

유니온 파인드 자료구조

유니온 파인드 자료구조는 집합 간의 합집합 연산 및 원소가 어떤 집합에 속해있는지를 찾는 연산을 효율적으로 처리하기 위해 사용된다. 해당 자료구조는 사이클을 판별하거나 연결성을 확인하는 문제에서 사용이 됨으로 크루스칼 알고리즘에서 사용된다.

유니온 파인드 자료구조에는 두 가지 주요 연산이 있는데, 바로 find와 union이다.

find(x) 연산을 한다고 하면, 원소 x가 속한 집합의 루트 노드를 찾는다.

union(x, y) 는 원소 x가 속한 집합과 원소 y가 속한 집합을 하나의 집합으로 병합한다.

처리 과정

1. 간선 리스트 작성: 그래프의 모든 간선과 그 가중치를 리스트로 나열한다.
2. 간선 정렬: 리스트의 가중치를 기준으로 오름차순으로 정렬한다.
3. 집합 초기화: 모든 정점을 각각 개별 집합으로 초기화한다.
4. 간선 선택: 정렬된 간선 리스트에서 가장 가중치가 작은 간선을 선택하여 트리에 추가한다. 단, 이 때 사이클이 발생하면 안된다.
   • 사이클 판별은 두 정점이 같은 집합에 속하는지 확인함으로 할 수 있다. 같은 집합에 속해있다는 것은 이미 연결되어있다는 말과 같기에 사이클이 발생한다.
5. 집합 병합: 선택된 간선으로 인해 연결된 두 정점을 하나의 집합으로 병합한다.
6. 반복: 모든 정점이 하나의 집합으로 병합될 때 까지 반복한다.

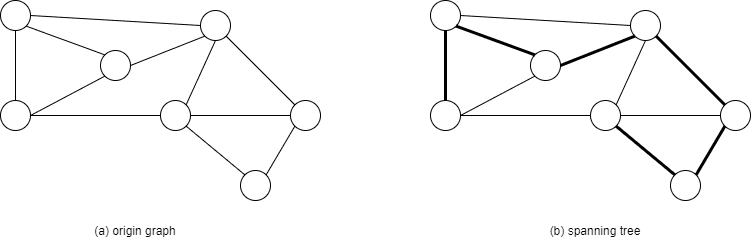
예제

아래와 같은 그래프가 있을 때, 크루스칼을 사용하여 최소 스패닝 트리를 만들어보자.

간선 리스트를 가중치의 오름차순으로 정렬해보면 아래와 같다:

집합을 초기화하는 것은 시각적으로 판별할 수 있기 때문에 해당 예제에서는 생략한다.
가장 가중치가 작은 간선은 정점 E와 G를 연결해주는 가중치 2의 간선이며, 이는 사이클을 발생시키지 않음으로 추가해준다.

이후 순차적으로 간선 리스트를 따라 간선을 추가해준다.

다음으로 가중치가 작은 간선은 E(A, D)이지만, 이는 사이클을 만들기 때문에 E(C, F)를 선택하여 이어준다.

마지막으로 정점 E와 D를 연결해주면 모든 정점이 포함된 집합, 즉 트리가 완성되며, 이 때의 총 가중치 합이 최소치임을 알 수 있다.

수도코드

# Union-Find 자료구조
def find_parent(parent, x):
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]

def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

# 크루스칼 알고리즘
def kruskal(graph):
    edges = []
    for node in graph:
        for neighbor, weight in graph[node]:
            edges.append((weight, node, neighbor))
    edges.sort()

    parent = [i for i in range(len(graph))]
    mst = []

    for edge in edges:
        weight, a, b = edge
        if find_parent(parent, a) != find_parent(parent, b):
            union_parent(parent, a, b)
            mst.append(edge)

    return mst

# 그래프 정의 및 실행 예시
graph = {
    'A': [('B', 7), ('D', 5)],
    'B': [('A', 7), ('D', 9), ('C', 8), ('E', 7)],
    'C': [('B', 8), ('E', 5)],
    'D': [('A', 5), ('B', 9), ('E', 15), ('F', 6)],
    'E': [('B', 7), ('C', 5), ('D', 15), ('F', 8), ('G', 9)],
    'F': [('D', 6), ('E', 8), ('G', 11)],
    'G': [('E', 9), ('F', 11)]
}

minimum_spanning_tree = kruskal(graph)
print(minimum_spanning_tree)