CS & 알고리즘 스터디: 두 번째 스터디

첫 번째 스터디 과제

첫 스터디를 하면서 ‘K번째 수’를 sort()를 안쓰고 풀기로 했고, stack, queue, graph를 직접 코드로 구현해보기로 했다.

K번째 수:

import sys

input = sys.stdin.readline

N, K = map(int, input().split())

A = list(map(int, input().split()))

def bubbleSort(A):
    changed = False
    for i in range(len(A)-1):
        if A[i] > A[i+1]:
            A[i], A[i+1] = A[i+1], A[i]
            changed = True            
    return changed

again = bubbleSort(A)

while again:
    again = bubbleSort(A)

print(A[K-1])

간단하게 버블소트로 구현해보았다.

스택:

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node* next;
} Node;

typedef struct Stack {
    Node* top;
} Stack;

Stack* createStack() {
    Stack* stack = (Stack*)malloc(sizeof(Stack));
    stack->top = NULL;
    return stack;
}

int isEmpty(Stack* stack) {
    return stack->top == NULL;
}

void push(Stack* stack, int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    if (newNode == NULL) {
        return;
    }
    newNode->data = data;
    newNode->next = stack->top;
    stack->top = newNode;
}

int pop(Stack* stack) {
    if (isEmpty(stack)) {
        return -1;
    }
    Node* temp = stack->top;
    stack->top = stack->top->next;
    int popped = temp->data;
    free(temp);
    return popped;
}

C로 구조체를 만들어 스택을 구현했다.

큐:

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node* next;
} Node;

typedef struct Queue {
    Node* front;
    Node* rear;
} Queue;

Queue* createQueue() {
    Queue* queue = (Queue*)malloc(sizeof(Queue));
    queue->front = queue->rear = NULL;
    return queue;
}

int isEmpty(Queue* queue) {
    return queue->front == NULL;
}

void enqueue(Queue* queue, int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    if (newNode == NULL) {
        return;
    }
    newNode->data = data;
    newNode->next = NULL;
    if (queue->rear == NULL) {
        queue->front = queue->rear = newNode;
        return;
    }
    queue->rear->next = newNode;
    queue->rear = newNode;
}

int dequeue(Queue* queue) {
    if (isEmpty(queue)) {
        return -1;
    }
    Node* temp = queue->front;
    int dequeued = temp->data;
    queue->front = queue->front->next;
    if (queue->front == NULL) {
        queue->rear = NULL;
    }
    free(temp);
    return dequeued;
}

큐 역시 비슷하게 구현했다. 정글에서 RB 트리를 비슷한 방식으로 구현해보았기에, 길지만 크게 어렵지는 않았다.

두 번째 스터디

키워드

그래프

Q: 그래프를 구현할 수 있는 두 가지 방법은?
A:

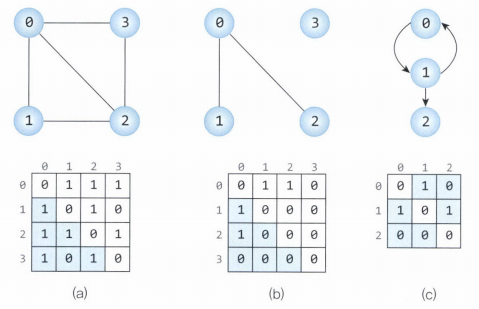
그래프를 구현할 수 있는 두 가지 대표적인 방법은 인접 행렬과 인접 리스트를 사용하는 것이다.
인접 행렬은 2차원 배열을 통해 일종의 테이블을 만들어 정점 간의 관계를 표시하는 방법으로 구현할 수 있다.
인접 행렬을 사용하면 행과 열로 표현된 정점들의 칸에 관계를 0 또는 1으로 설정하는 것으로 빠르게 간선을 표현할 수 있으며 간선의 존재를 확인하기 쉽지만, 메모리 사용량이 높다는 단점이 있다.

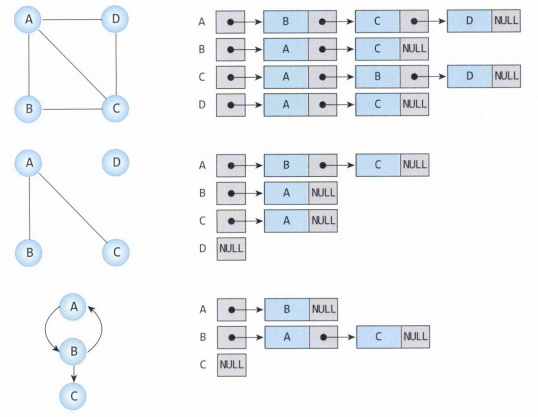
인접 리스트 또한 2차원 배열을 사용하지만, 관계가 없는 정점들은 무시하고 간선이 존재하는 정점들만 리스트에 삽입한다. 이는 메모리를 효율적으로 사용하도록 해주지만, 간선이 많아질 수록 탐색이 오래 걸린다는 단점이 있다.

Q: 각 방법에 대해, “두 정점이 연결되었는지” 확인하는 시간복잡도와 “한 정점에 연결된 모든 정점을 찾는” 시간복잡도, 그리고 공간복잡도를 비교해 주세요.
A:

인접 행렬:
두 정점이 연결되었는지 확인하는 시간 복잡도: O(1)

• 인접 행렬 adj가 주어졌을 떄, 단순히 adj[u][v]를 검사하면 연결 여부를 확인할 수 있다.

한 정점에 연결된 모든 정점을 찾는 시간 복잡도: O(V), V는 정점의 개수

• 특정 정점 u에 대해 연결된 모든 정점을 찾기 위해서는 u행 adj[u]를 검사해야 하기 떄문에 V개의 정점을 모두 확인해야 한다.

공간복잡도: O(V²)

• 인접 행렬은 2차원 배열로 구현되어 V * V 크기의 배열을 사용한다.

인접 리스트:
두 정점이 연결되었는지 확인하는 시간복잡도: 평균적으로 O(E/V)

• 인접 리스트에서는 정점 u에 대해 연결된 정점들의 리스트를 순회하여 정점 v가 연결되어 있는지 확인해야 한다. 모든 정점을 순회해야 하면 최악의 시간 복잡도 O(V)가 된다.

한 정점에 연결된 모든 정점을 찾는 시간복잡도: O(E/V)

• 특정 정점 u에 대해 연결된 모든 정점을 찾는 시간 복잡도는 연결된 정점의 개수에 비례한다. 이는 인접 행렬보다 평균적으로 빠르지만, 최악의 경우에는 O(V)이다.

공간복잡도: O(V + E)

• 인접 리스트는 각 정점에 대해 연결된 정점들의 리스트를 저장기 때문에, 정점의 수 V와 간선의 수 E에 비례하는 공간을 사용한다.

이에 따라, 연결이 많은 그래프에는 인접 행렬이, 희소한 그래프에는 연결 리스트가 적합하다.

Q: 그래프에서 최단거리를 구하는 방법은?
A:

그래프에서 최단 거리를 구하는 방법은 그래프의 유형에 따라 달라진다. 가중치가 있는 간선인지, 음수 가중치가 존재하는지에 따라 적절한 알고리즘을 선택해야 한다. 대표적인 최단거리 탐색 알고리즘에는 다익스트라 알고리즘, 플로이드-워셜 알고리즘 등이 있다.

다익스트라 알고리즘 (Dijkstra’s Algorithm): 다익스트라 알고리즘은 그래프의 단일 출발점에서 모든 다른 정점까지의 최단 거리를 찾는 데 사용된다.

플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm): 플로이드-워셜 알고리즘은 모든 정점 쌍 간의 최단 거리를 찾는 데 사용되며, 음수 가중치 간선을 허용한다. 다만, 음수 사이클이 존재해서는 안된다.

Q: 정점의 개수가 N개, 간선의 개수가 N^3개라면 어떤 알고리즘이 효율적일까요?

그래프 탐색

Q: DFS와 BFS의 수도코드를 작성해주세요.
A:

DFS:

def dfs(graph, start_node):
    visited = set()
    stack = [start_node]
    
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            process(node)
            
            for neighbor in reversed(graph[node]):
                if neighbor not in visited:
                    stack.append(neighbor)

BFS:

from collections import deque

def bfs(graph, start_node):
    queue = deque([start_node])
    visited = set([start_node])
    
    while queue:
        node = queue.popleft()
        process(node)
        
        for neighbor in graph[node]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

MST

Q: 크루스칼 알고리즘에서 사용하는 Union-Find 자료구조에 대해 설명해 주세요.
A:

유니온 파인드 자료구조는 Union과 Find라는 기본 연산을 지원하는 자료구조이다.

Find: 특정 원소가 어떤 집합에 속해 있는지 확인하는 연산이다. 해당 원소가 속한 집합의 루트 노드를 찾을 수 있다.

Union: 두 집합을 하나로 합치는 연산이다. 두 개의 원소가 서로 다른 집단에 속해 있을 때, 하나의 집합으로 합친다.

유니온 파인드 자료구조를 사용함으로 크루스칼 알고리즘에서의 사이클을 방지할 수 있다.

Q: 크루스칼과 프림 알고리즘를 비교해보세요.

크루스칼 알고리즘과 프림 알고리즘의 차이는 그래프의 MST를 찾는 과정에 있다.

Thread Safe

Thread Safe란 무엇인가요?

Thread Safe란 여러 스레드가 동시에 하나의 자원에 접근할 때 야기될 수 있는 문제를 해결하기 위해 설계된 자료구조, 또는 소프트웨어의 성질이다.

멀티스레드 환경에서 여러 스레드가 하나의 함수에 동시에 접근을 해도 프로그램의 실행에 문제가 없음을 의미한다. 즉 예상 외 동작이나 레이스 컨디션, 데이터 오염 등이 모두 일어나지 않는다는 말이다.

사용하고 있는 언어의 자료구조는 Thread Safe 한가요? 그렇지 않다면, Thread Safe 한 Wrapped Data Structure 를 제공하고 있나요?

자바스크립트라는 언어는 기본적으로 싱글스레드로 동작하는 언어이기 때문에 Thread Safety를 고려하지 않고 설계되어있다.

싱글스레드로 동작는 언어이기 때문에 애초에 문제 자체가 발생하지 않을 것으로 생각할 수 있지만, 특정 상황에서는 이를 고려해야 한다. Promise, Async/Await과 같이 비동기적으로 실행되는 코드에서는 여러 작업이 동시에 진행될 수 있으며, 이 때 같은 공유 자원에 대한 접근이 동기화되어 있지 않다면 예기치 못한 결과가 발생할 수 있다. 여기에 더해 라이브러리나 프레임워크는 멀티스레드 환경에서 동작할 수 있기 때문에 Thread Safety를 고려하는 것이 타당하다.

자바스크립트에서는 별도의 자료구조보다는 Locks 또는 Mutex를 통해 임게구역에 대한 접근을 제어하여 한 시점에 하나의 스레드에만 접근을 허용하면 레이스 컨디션이나 데이터 오염을 방지할 수 있다.

번외: Java

synchronized 키워드를 사용하면 Thread Safe하게 만들 수 있다.
메서드 또는 객체를 기준으로 적용이 가능하다.

그리디

그리디 포스트

Q: 그리디 수도코드를 작성해주세요.
A:

GreedyAlgorithm(Input):
    Initialize an empty set S  // 또는 다른 자료구조를 초기화
    while (termination condition is not met):
        Select the best element x from Input that gives the highest (or lowest) immediate benefit
        Add x to S (or take the appropriate action)
        Update Input (remove elements covered by x or modify Input if necessary)
    
    return S (or the result of the actions taken)

Q: 그리디 알고리즘은 어떤 경우에 사용할 수 있을까요?
A:

그리디 알고리즘은 주어진 문제에서 매 순간 최적의 선택을 함으로 국부적인 해를 구하고, 이를 통해 전체 문제의 최적해를 구할 수 있는 경우에 사용된다.

동적 계획법

동적 계획법 포스트

Q: 동적 계획법의 두 가지 방식을 비교해보세요.
A:

	Top-Down	Bottom-Up
구현	재귀	반복문
저장 방식	메모이제이션	타뷸레이션

자세한 비교는 동적 계획법 포스트에서 확인 가능합니다.

Q: 동적 계획법은 어떤 경우에 사용할 수 있을까요?
A:

동적 계획법은 큰 문제를 작은 부분 문제로 나누어 각 부분 문제의 최적해를 사용하여 전체 문제의 해를 구할 수 있을 때 사용된다. 특히, 부분 문제가 중복적으로 발생하는 경우에 이를 저장함으로 반복 계산을 방지하여 효율을 최적화할 수 있다. 이는 최단 경로 문제, LCS, 0-1 배낭 문제 등의 문제를 푸는 데에 사용될 수 있게 해준다.

문제 풀이

그래프 & 그래프 탐색

음식물 피하기

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

N, M, K = map(int, input().split())

graph = [[0]*M for _ in range(N)]
visited = [[False]*M for _ in range(N)]
ans = 0

for i in range(K):
    n, m = map(int, input().split())
    graph[n-1][m-1] = 1

dx = [0,1,0,-1]
dy = [1,0,-1,0]

def dfs(x, y):
    global count
    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]
        if(0 <= nx < N and 0 <= ny < M):
            if graph[nx][ny] == 1 and not visited[nx][ny]:
                visited[nx][ny] = True
                count += 1
                dfs(nx, ny)

for i in range(N):
    for j in range(M):
        if graph[i][j] == 1 and not visited[i][j]:
            count = 0
            dfs(i, j)
            ans = max(ans, count)

print(ans)

MST

네트워크 연결

import sys

input = sys.stdin.readline

def find(a):
    if a == parent[a]:
        return a
    parent[a] = find(parent[a]) 
    return parent[a]

def union(a, b):
    a = find(a)
    b = find(b)
    if b < a:
        parent[a] = b
    else:
        parent[b] = a

n = int(input())
m = int(input())
arr = []
parent = [i for i in range(n + 1)]
res = 0
for i in range(m):
    a, b, c = map(int, input().split())
    arr.append((
        c,
        a,
        b,
    ))

arr.sort(key=lambda x: x[0])
for dis, a, b in arr:
    if find(a) != find(b):
        union(a, b)
        res += dis
print(res)

그리디

A->B

import sys  

input = sys.stdin.readline

A, B = map(int, input().split()) 
count = 1

while B != A:
    count += 1
    b = B

    if b%10 == 1:
        b//= 10
    elif b%2 ==0:
        b//= 2

    if b == B:
        print(-1)
        break

    B = b 
else: 
    print(count)

카드 정렬하기

import heapq
import sys
input = sys.stdin.readline

n = int(input()) 
priority_queue = [] 
result = 0

for _ in range(n):
    heapq.heappush(priority_queue, int(input()))  

if len(priority_queue) == 1: 
    print(0)
else:  
    while priority_queue: 
        if len(priority_queue) == 2:  
            print(result + sum(priority_queue))  
            break
        temp = heapq.heappop(priority_queue) + heapq.heappop(priority_queue) 
        heapq.heappush(priority_queue, temp) 
        result += temp  

동적 계획법

연속합

n = int(input())
m = list( map(int, input().split(' ')))
 
for i in range(1, n):
    m[i] = max(m[i], m[i] + m[i-1])
    
print(max(m))